数学思维与方法在高中生物教学中的应用——以不同氧浓度下细胞呼吸作用CO2释放量与O2吸收量的关系图为例

　　作者：赖增隆(Lai Zeng Long)

　　摘要：高中生物“细胞呼吸”一节是教学的重点也是难点。细胞呼吸作用的强度受多个因素影响，其中氧气浓度是影响植物呼吸作用强度的重要因素之一[1]。而纯文字的定性叙述难以准确表达其背后的生物学原理，更不能体现生物学科的理科特点。本文运用数学思维与方法，进行模型构建定量分析，使学生能加深对细胞呼吸过程的理解，培养学生的理性思维和严谨的科学态度。

　　关键词：数学思维与方法 数学模型 生物教学 细胞呼吸

　　高中生物教学过程中常常会遇到一些难题，纯文字的定性叙述难以准确表达背后的生物学原理，老师教起来难，学生理解起来也难。比如：关于氧气浓度与有氧呼吸、无氧呼吸关系的曲线图分析：二氧化碳的最值问题?为何储存植物器官一般置于氧气浓度为5%的环境中?当二氧化碳释放量最少时，有氧呼吸速率是否等于无氧呼吸速率? 等问题更是困扰师生的难点。比如以下例题：

　　例题1：将质量相同(足量)的苹果肉分别放在O2浓度不同的密闭容器中，1h后测定O2的吸收量和CO2的释放量，结果如表所示，由此得出的判断不正确的是(　　)

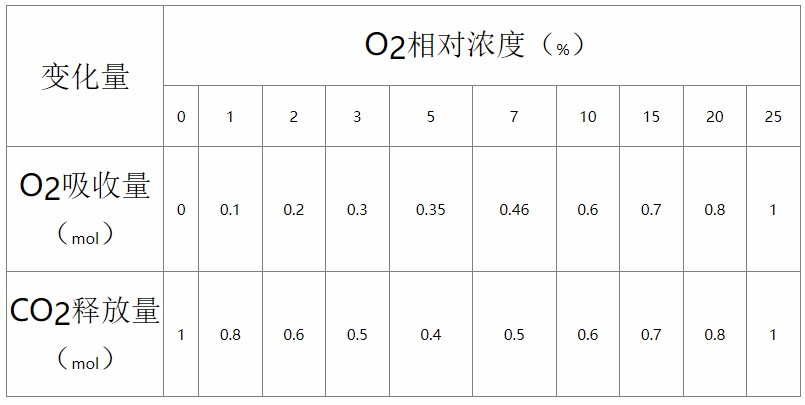
　　A. O2浓度为2%时苹果细胞进行无氧呼吸和有氧呼吸

　　B. 果肉在O2浓度为3%时每小时分解葡萄糖0.15 mol

　　C. 贮藏苹果的环境中，适宜的O2浓度为5%

　　D. O2浓度为5%时无氧呼吸和有氧呼吸强度均最弱

　　例题2：如图所示酵母菌的呼吸作用与氧气浓度的关系.下列说法不正确的是(　　)

　　1. 有氧呼吸过程二氧化碳释放量(或氧气吸收量)随密闭容器中氧气体积百分比的变化方程的拟合

　　本文作者认为对于该问题的解决可以借助食品工程专业的实验数据与论文结论运用数学思维与方法进行定量分析加以解决。上海水产大学食品学院刘晓丹，谢晶通过研究对香菇在不同温度条件下密闭容器中氧气和二氧化碳随时间浓度变化进行测定，通过酶动力学原理和利用非线性估算法、多重回归分析分别获得气体成分的变化曲线并获得相应参数。以时间为自变量，拟合[O2]、[CO2]浓度随时间变化的方程，同时引入米氏方程的非竞争性作用的速度方程充分考虑两种气体之间的可能关系，大大简化了由于细胞呼吸作用导致的体系的复杂性，提高实验数据与结论的可信度，拟合的方程复相关系数均达到0.95以上[3]。方程如下：

　　[O2]=21-B1×arctan(A1*t) (1)

　　[CO2]=B2×arctan(A2*t) (2)

　　由(1)可知，有氧呼吸消耗的氧气随时间变化的方程应为[O2]= B1×arctan(A1*t) (3)其中实验测定[O2][CO2]的时间t 相同，消去t可得[CO2]与[O2]的关系方程：

　　设[O2]=x [CO2]=y (x、y均表示体积百分比) 由方程(2)、(3)变形得:

　　arctan(A1*t)=x/B1

　　arctan(A2*t)=y/B2

　　∴ A1*t=tan(x/B1 ) A2*t=tan(y/B2)

　　t取相同值∴ t=tan(x/B1 )/A1 t=tan(y/B2)/ A2

　　∴ tan(x/B1 )/A1 =tan(y/B2)/ A2

　　∴ y= B2× arctan{ A2/A1*tan(x/B1 )} x∈(0 +∞)

　　根据论文选取相应参数：A1=0.066 B1=19.33 A2=0.00042 B2=1073.7 以0.01为梯度差给X赋值，代入上述方程可以算出相应的y值，根据计算得出的2100个y 值可以拟合出有氧呼吸过程二氧化碳释放量(或氧气吸收量)随密闭容器中氧气体积百分比的变化方程：

　　y1 = 10-3x3 - 10-2x2 + 0.42x x∈[0 +∞) R2 = 0.9996 (4)

　　2. 无氧呼吸过程释放二氧化碳的量随密闭容器中氧气体积百分比变化曲线方程的计算

　　例题3：呼吸熵(RQ)指单位时间内进行细胞呼吸的生物释放二氧化碳量与吸收氧气量的比值(RQ=释放的二氧化碳体积/消耗的氧气体积).如图是生物氧化分解葡萄糖过程中氧分压与呼吸熵的关系.以下叙述中，正确的是(　　)

　　A. 呼吸熵越大，细胞有氧呼吸越强，无氧呼吸越弱

　　B. B点有氧呼吸的强度大于A点有氧呼吸的强度

　　C. 为延长水果保存的时间，最好将氧分压调至C点

　　D. C点以后，细胞呼吸强度不随氧分压的变化而变化

　　图中曲线的形状与反比例函数在第一象限的图像很相似，因此可以设该方程为：y=k/x ; 根据呼吸熵的定义 RQ=[CO2]/[O2]，在以葡萄糖作为呼吸作用的底物时，有氧呼吸消耗的氧气等于其放出的二氧化碳，RQ-1=([CO2]-[O2])/[O2]，则无氧呼吸释放的二氧化碳随密闭容器中氧气体积百分比的变化曲线可以表示为y=k/x-1，无氧呼吸在不同氧气体积百分比环境下所释放二氧化碳的量可表示为(RQ-1)* [O2];已知当氧气体积百分比达到10%时无氧呼吸消失，即该曲线过点(10，0)，代入上述方程可知k=10，故无氧呼吸释放二氧化碳与密闭容器中氧气体积百分比的关系可表示为 :

　　y=10/x-1 x∈(0 +∞)

　　无氧呼吸释放二氧化碳的量可表示为：

　　y2=(10/x-1)* y1 x∈(0 +∞) (5)

　　3. 对不同氧气体积百分环境下细胞呼吸作用过程CO2释放量与O2吸收量的关系解释

　　结合方程(4)、(5)，当密闭容器中氧气体积百分比相同时即x取值相同时，密闭容器中二氧化碳的总量：Y=y1 + y2

　　即Y=10y1 /x=(10-2x3 - 10-1x2 + 4.2x )/x x∈(0 +∞)

　　化简：Y= 10-2x2 - 10-1x + 4.2 x∈(0 +∞)

　　此方程可以很好的解释为何在氧气含量为5%的环境中储存植物器官最好，因为此方程在x=5时(即密闭容器氧气体积百分比为5%)可以取到最小值，即密闭容器中总二氧化碳量的最小值，代表此时植物细胞呼吸作用释放的总二氧化碳量最少，有机物消耗最少，有利于保存植物器官。由方程(5)还可作进一步推论： y2/ y1 =(10/x-1)，当x=5时，可知 y1 = y2 此时y1和y2可分别表示以葡萄糖作为细胞呼吸作用底物时相同的单位时间内有氧呼吸吸收的氧气量和无氧呼吸释放的二氧化碳量，也就是有氧呼吸速率与无氧呼吸速率相等。因此对于细胞呼吸(以葡萄糖为底物)释放二氧化碳的量与氧气浓度的关系曲线图本文作者更认同以下类型。

　　在上述问题的解决过程中合理利用数学思维与方法，通过数学建模的方式把生物学问题转化为数学问题，大大简化了由于呼吸作用过程多步骤，多种酶参与等因素导致的体系复杂性，通过定量分析对生物学现象进行解释，可以很好的达成运用数学思维与方法进行简化处理、进行模型构建令学生能加深理解、培养学生的理性思维和严谨的科学态度等目标。

　　参考文献：

　　[1]张汞.寻根究源解决生物难点.中学生物学,2015(9)：55-56.

　　[2]陆文锋.数学方法在高中生物教学中的应用.华南师范大学学报,2010(4):66-68.

　　[3]刘晓丹，谢晶.利用酶动力学拟合在密闭条件下香菇呼吸速率方程及米氏方程.中国食品学报,2006(1)：1074-1078.